|
|
||
|---|---|---|
| .giteat/workflows | ||
| .RData | ||
| .Renviron | ||
| .Rhistory | ||
| .gitignore | ||
| .httr-oauth | ||
| Dockerfile | ||
| README.md | ||
| _auth0.yml | ||
| app.R | ||
| arbre1.png | ||
| arbre2.png | ||
| docker-launcher.exe | ||
| example_document.docx | ||
| my_dataset.csv | ||
| test_app.zip | ||
README.md
Projet de création d’une plateforme d’automatisation de tests statistiques
Introduction
Le but de cette plateforme est d’automatiser les traitements statistiques permettant d’étudier les différences existantes entre plusieurs groupes. Avant de voir quels sont les tests effectués, nous commencerons par faire un rappel des notions de base à avoir pour interpréter ces tests.
Prérequis
- Hypothèse nulle (H0) : L'hypothèse de départ à tester. Elle est généralement formulée comme une égalité ou une absence de différence significative entre les groupes.
- Hypothèse alternative (H1 ou Ha) : L'hypothèse que vous voulez prouver, généralement formulée comme une différence ou une inégalité significative entre les groupes.
- Niveau de signification (α) : Le seuil de probabilité en dessous duquel vous rejetterez l'hypothèse nulle. Il est souvent fixé à 0,05, ce qui signifie que vous acceptez un risque de 5 % de commettre une erreur de type I.
- P-valeur : La probabilité d'obtenir des résultats aussi extrêmes que ceux observés si l'hypothèse nulle est vraie. Une p-valeur faible (généralement < α) suggère que vous pouvez rejeter l'hypothèse nulle.
Les tests
Dans un premier temps, les tests choisis ont été les suivants :
- Shapiro
- Levene
- Barlett
- Fisher
- Wilcoxon
- Student
- Welch
- Anova
- Emmeans
- Krustal-Wallis
Shapiro
Le test de Shapiro est un test permettant d’évaluer la normalité d’une distribution. L’hypothèse H0 ici est que la distribution est normale. Ainsi, on estime que la distribution est normale sauf si l’on trouve une p-value inférieure à notre niveau de signification.
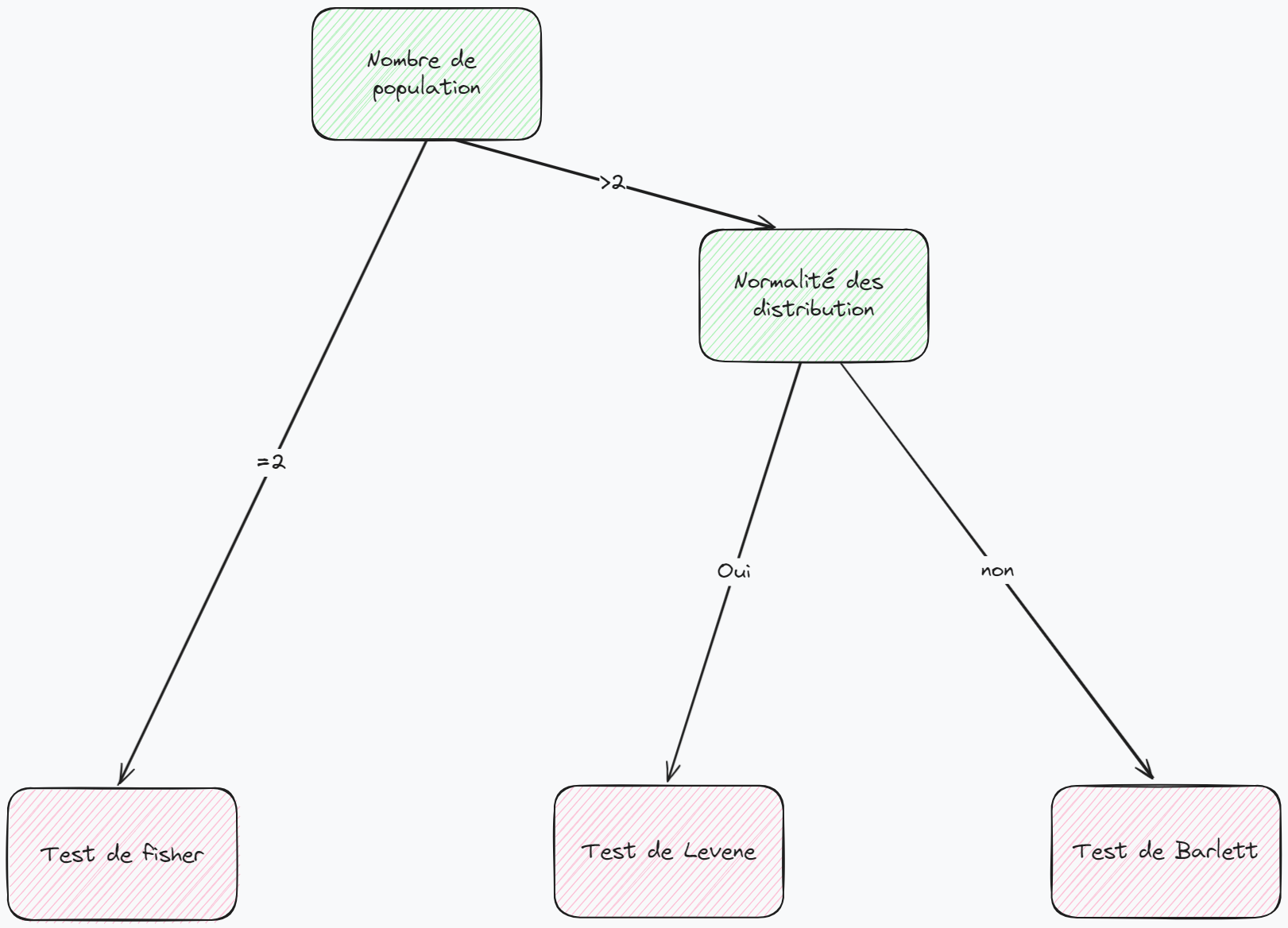
Levene
Le test de Levene est un test non paramétrique, il ne présuppose aucune distribution, permettant de comparer les variances de plusieurs échantillons. L’hypothèse H0 est l’homoscédasticité des populations. Ainsi, on estime les variances égales sauf si l’on trouve une p-value inférieure à notre niveau de signification.
Barlett
Le test de Barlett est un test paramétrique, il présuppose une distribution, permettant de comparer les variances de plusieurs échantillons. L’hypothèse H0 est l’homoscédasticité des populations. Ainsi, on estime les variances égales sauf si l’on trouve une p-value inférieure à notre niveau de signification.
Fisher
Le test de Fisher est un test non paramétrique, il ne présuppose aucune distribution, permettant de comparer les variances de deux échantillons. L’hypothèse H0 est l’homoscédasticité des deux populations. Ainsi, on estime les variances égales sauf si l’on trouve une p-value inférieure à notre niveau de signification.
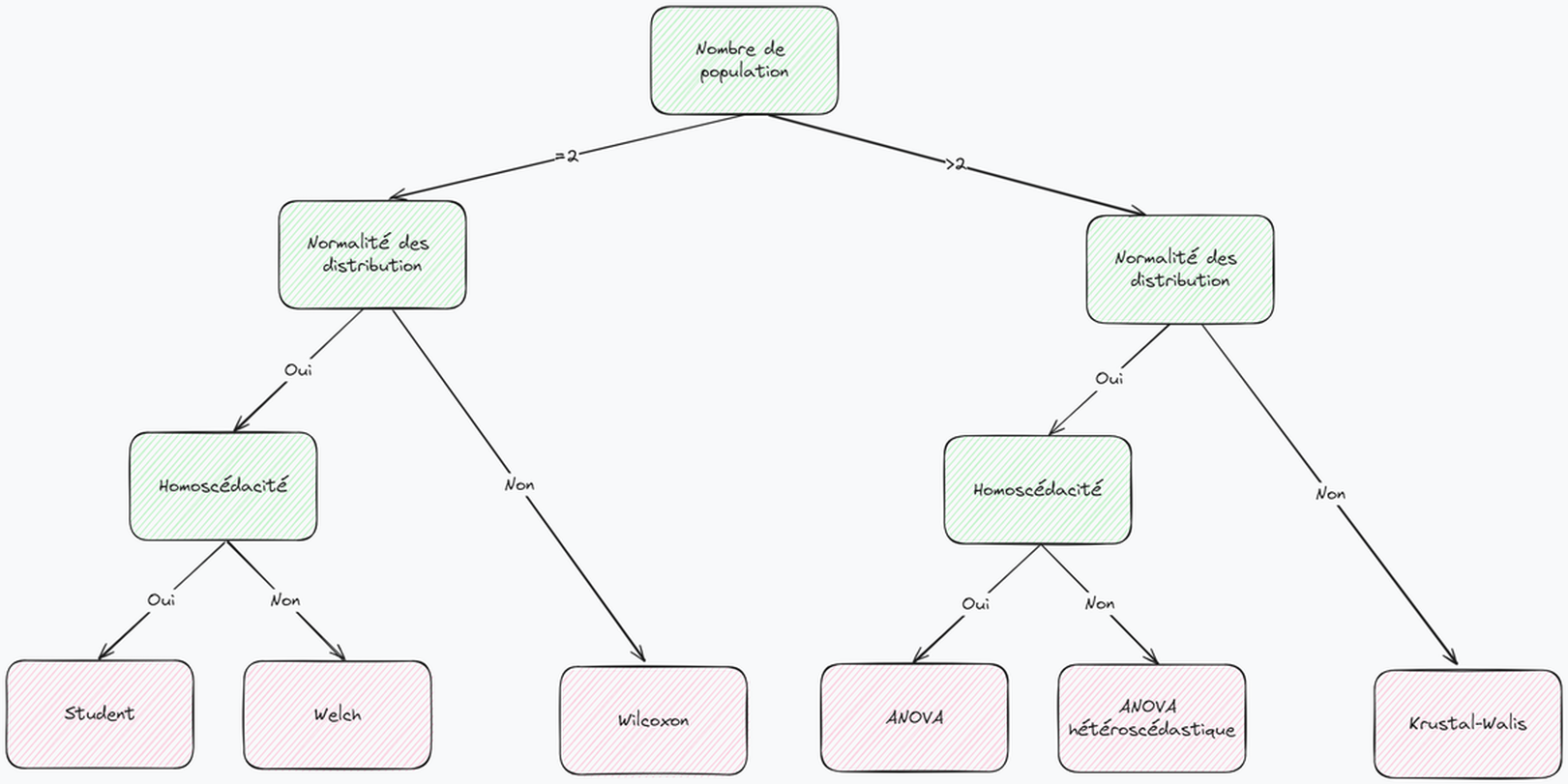
Wilcoxon
Le test de Wilcoxon est un test non paramétrique, il ne présuppose aucune distribution, permettant de comparer la moyenne de deux échantillons. L’hypothèse H0 est l’égalité des moyennes des deux populations. Ainsi, on estime les moyennes égales sauf si l’on trouve une p-value inférieure à notre niveau de signification.
Student
Le test de Student est un test paramétrique, il présuppose une distribution normale et une égalité des variances, permettant de comparer la moyenne de deux échantillons. L’hypothèse H0 est l’égalité des moyennes des deux populations. Ainsi, on estime les moyennes égales sauf si l’on trouve une p-value inférieure à notre niveau de signification.
Welch
Le test de Welch est un test paramétrique, il présuppose une distribution, permettant de comparer la moyenne de deux échantillons. L’hypothèse H0 est l’égalité des moyennes des deux populations. Ainsi, on estime les moyennes égales sauf si l’on trouve une p-value inférieure à notre niveau de signification.
ANOVA
L'ANOVA est un test paramétrique, présupposant la normalité de la distribution ainsi que l’égalité des variances, utilisée pour comparer les moyennes de trois groupes ou plus pour déterminer si au moins un groupe est statistiquement différent des autres. L’hypothèse H0 est l’égalité de toutes les moyennes, l’hypothèse H1 est donc « Il existe au moins une moyenne de groupe différente des autres ». Ainsi, on estime les moyennes égales sauf si l’on trouve une p-value inférieure à notre niveau de signification.
Emmeans
Le test Emmeans est utilisé après avoir rejeté l’hypothèse nulle lors d’une ANOVA. Il permet de déterminer les groupes se différenciant les uns des autres.
Krustal-Wallis
Le test de Krustal-Wallis est un test non paramétrique, ne présupposant pas la normalité de la distribution, utilisée pour comparer les moyennes de trois groupes ou plus pour déterminer si au moins un groupe est statistiquement différent des autres. L’hypothèse H0 est l’égalité de toutes les moyennes, l’hypothèse H1 est donc « Il existe au moins une moyenne de groupe différente des autres ». Ainsi, on estime les moyennes égales sauf si l’on trouve une p-value inférieure à notre niveau de signification.
Nous pouvons donc résumer les cas d’utilisations des différents tests de comparaison des moyennes à l’aide de l’arbre de décision.
Afin de tester la normalité des distributions nous utiliserons, dans tous les cas, un test de Shapiro sur chacune des variables quantitatives. Pour tester l’homoscédasticité l’arbre de décision suivant :